3405. Almost
Shortest Path
Finding
the shortest path that goes from a starting point to a destination point given
a set of points and route lengths connecting them is an already well known
problem, and it's even part of our daily lives, as shortest path programs are
widely available nowadays.
Most
people usually like very much these applications as they make their lives
easier. Well, maybe not that much easier.
Now
that almost everyone can have access to GPS navigation devices able to
calculate shortest paths, most routes that form the shortest path are getting
slower because of heavy traffic. As most people try to follow the same path,
it's not worth it anymore to follow these directions.
With
this in his mind, your boss asks you to develop a new application that only he
will have access to, thus saving him time whenever he has a meeting or any
urgent event. He asks you that the program must answer not the shortest path,
but the almost shortest path. He defines the almost shortest path as the
shortest path that goes from a starting point to a destination point such that
no route between two consecutive points belongs to any shortest path from the
starting point to the destination.
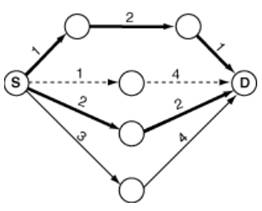
For
example, suppose the figure below represents the map given, with circles representing
location points, and lines representing direct, one-way routes with lengths
indicated. The starting point is marked as S and the destination point is
marked as D. The bold lines belong to a shortest path (in this case there are
two shortest paths, each with total length 4). Thus, the almost shortest path
would be the one indicated by dashed lines (total length 5), as no route
between two consecutive points belongs to any shortest path. Notice that there
could exist more than one possible answer, for instance if the route with
length 3 had length 1. There could exist no possible answer as well.
Input. The input contains several test cases. The first line
of a test case contains two integers n
(2 ≤ n ≤ 500) and m (1 ≤ m ≤ 104), separated by a single space, indicating
respectively the number of points in the map and the number of existing one-way
routes connecting two points directly. Each point is identified by an integer
between 0 and n – 1. The second line
contains two integers s and d, separated by a single space,
indicating respectively the starting and the destination points (s ≠ d; 0 ≤ s, d < n).
Each one of the following m lines contains three integers u,
v and p (u ≠ v, 0 ≤ u, v < n, 1 ≤ p ≤ 103), separated by single spaces, indicating
the existence of a one-way route from u
to v with distance p. There is at most one route from a
given point u to a given point v, but notice that the existence of a
route from u to v does not imply there is a route from v to u, and, if such road
exists, it can have a different length. The end of input is indicated by a line
containing only two zeros separated by a single space.
Output. For each test case in the input, your program must
print a single line, containing -1 if it is not possible to match the
requirements, or an integer representing the length of the almost shortest path
found.
|
Sample Input |
Sample Output |
|
7 9 0 6 0 1 1 0 2 1 0 3 2 0 4 3 1 5 2 2 6 4 3 6 2 4 6 4 5 6 1 4 6 0 2 0 1 1 1 2 1 1 3 1 3 2 1 2 0 3 3 0 2 6 8 0 1 0 1 1 0 2 2 0 3 3 2 5 3 3 4 2 4 1 1 5 1 1 3 0 1 0 0 |
5 -1 6 |
РЕШЕНИЕ
алгоритм Дейкстры
Анализ
алгоритма
Задан ориентированный взвешенный граф, в
котором выделены две вершины s и t. Пусть величина кратчайшего пути от s к t
равна d. Почти
кратчайшим путем от s к t называется такой путь наименьшей
стоимости, который не проходит ни по одному ребру, по которому может проходить
путь длины d. В задаче следует найти
длину почти кратчайшего пути или вывести -1 если такого пути не существует.
Запустим
алгоритм Дейкстры из вершины s на
заданном графе и из вершины t на обратном. Построим два массива dist и distR, где dist[i] равно
длине кратчайшего пути от s до i, а distR[i] равно
длине кратчайшего пути от i до t. Все
ребра, которые могут лежать на кратчайшем пути, занесем в массив
множеств avoid: avoid[i] содержит
такое множество вершин j, что через
ребро (i, j) длины w может проходить кратчайший путь. Это возможно, если
только имеет место равенство:
dist[i] + w + distR[j] == dist[f]
Осталось еще
один раз запустить алгоритм Дейкстры по ребрам, не входящих в avoid. Найденный
путь и будет почти кратчайшим. Его длина будет строго меньше d.
Реализация
алгоритма
#include <cstdio>
#include <cstring>
#include <vector>
#include <set>
#include <queue>
#define MAX 502
#define INF 0x3F3F3F3F
using namespace
std;
int i, n, m, s, f, b, e, w;
int used[MAX], parent[MAX];
int d, u, v;
vector<set<int> >
avoid;
struct edge
{
int node, dist;
edge(int node, int dist) :
node(node), dist(dist) {}
};
bool operator<
(edge a, edge b)
{
return a.dist > b.dist;
}
vector<vector<edge> > g, gr;
vector<int> dist,
distR;
void path(int
v)
{
if (parent[v] == -1) return;
avoid[parent[v]].insert(v);
path(parent[v]);
}
int
Dijkstra(vector<vector<edge> > &g, vector<int> &dist,
int s, int f)
{
dist = vector<int>(n,INF);
dist[s] = 0;
memset(parent,-1,sizeof(parent));
memset(used,0,sizeof(used));
priority_queue<edge> pq;
pq.push(edge(s,0));
while(!pq.empty())
{
edge e = pq.top();
pq.pop();
int v = e.node;
if (v == f) return
dist[f];
if (e.dist > dist[v]) continue;
for(int i = 0; i <
g[v].size(); i++)
{
int to = g[v][i].node;
int cost = g[v][i].dist;
if (avoid[v].find(to) != avoid[v].end()) continue;
if (!used[to] && dist[to] > dist[v] +
cost) // Relaxation
{
dist[to] =
dist[v] + cost;
pq.push(edge(to,dist[to]));
parent[to] = v;
}
}
}
return -1;
}
int main(void)
{
while(scanf("%d
%d",&n,&m), n + m)
{
scanf("%d %d",&s,&f);
g.clear();
g.resize(n);
gr.clear();
gr.resize(n);
avoid.clear();
avoid.resize(n);
for(i = 0; i < m; i++)
{
scanf("%d %d %d",&b,&e,&w);
g[b].push_back(edge(e,w));
gr[e].push_back(edge(b,w));
}
d =
Dijkstra(g,dist,s,f);
d =
Dijkstra(gr,distR,f,s);
for(u = 0; u < g.size(); u++)
{
for(i = 0; i < g[u].size(); i++)
{
v =
g[u][i].node;
w =
g[u][i].dist;
if (dist[u] + w + distR[v] == dist[f])
avoid[u].insert(v);
}
}
d =
Dijkstra(g,dist,s,f);
printf("%d\n",d);
}
return 0;
}